Rhombic Triacontahedron
Nov 13 2016 Sun
5:02 pm PHT
I’ve mentioned in passing here on this blog that my favorite number is the golden ratio. If you know me, this should not be surprising at all. Two of my favorite school subjects are math and art after all, and aside from fractals (which I also really love), the golden ratio is a concept that straddles both fields, having numerous interesting mathematical properties and being used as an aesthetically pleasing proportion in the arts and architecture. I’m quite sure that I am far from alone in having the golden ratio as their favorite number.
While fractals and the golden ratio provide countless beautiful geometric figures and shapes, I’ve never really had one that I can consider as my most favorite shape. There are several fractals that I like and two of them are the famous Mandelbrot set and the Heighway dragon curve. And the golden ratio has many associated shapes, the golden spiral being the most well-known.
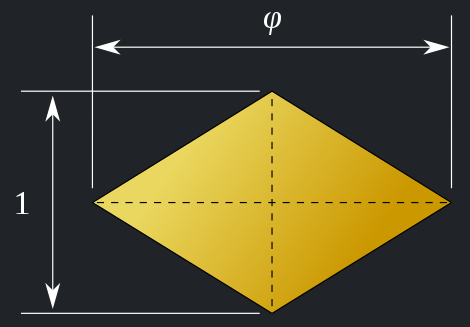
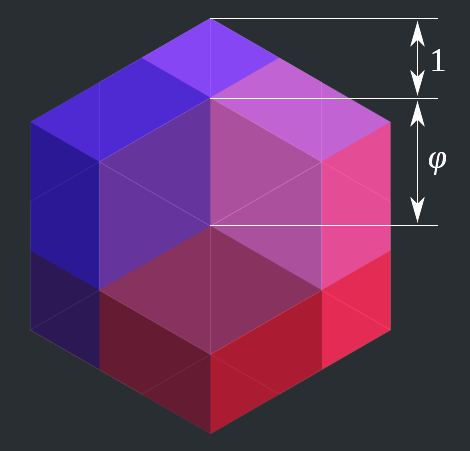
Given the many beautiful shapes available, it was only late last year that I finally selected one geometric shape as my most favorite: the rhombic triacontahedron (shown above). This is a three-dimensional, 30-sided ("triaconta-”) convex polyhedron (”-hedron”) having identical rhombuses ("rhombic”) as its faces. But what’s interesting is that all of these 30 rhombuses are golden rhombuses, that is, their two diagonals are in the golden ratio.
I have to admit with some embarrassment that it was only last year that I became aware of this polyhedron and its numerous connections to the golden ratio. (It’s not just the rhombuses.) I’ve known for quite a while now that the more familiar icosahedron is connected to the golden ratio: if you arrange three golden rectangles such that they are intersecting with their centers coincident and mutually perpendicular to each other, their combined 12 corners coincide with the vertices of the icosahedron. (I actually used this knowledge to create a stable stellated icosahedron as a Christmas lantern back in high school.) The dodecahedron, being the dual of the icosahedron and having regular pentagons as its faces, is also connected to the golden ratio: the ratio of a pentagon’s edge to its diagonal is golden. And if you dually combine the icosahedron and the dodecahedron such that their edges intersect, their combined vertices are the vertices of the rhombic triacontahedron. This also means that the icosahedron’s and dodecahedron’s edges, being coincident with with the diagonals of the golden rhombuses, are in a golden ratio. Not only that, but various orthogonal projections of this remarkable polyhedra also contain various lengths in a golden ratio.
It’s therefore no surprise that I’ve selected the rhombic triacontahedron as my favorite shape. It incorporates the golden ratio, my favorite number, in numerous fascinating ways, much like the way the golden ratio itself appears in many unexpected and amazing places.
You can explore this shape a bit by checking out this simple web app that I designed to help me create most of the illustrations on this blog post.


Comments
Comments are currently disabled.